There is enough known about cloud formation that replicating its mechanism has become a staple of the school science project scene. But a new study by scientists at the U.S. Department of Energy’s Lawrence Berkeley National Laboratory (Berkeley Lab) reveals that much more is going on at the microscopic level of cloud formation than previously thought.
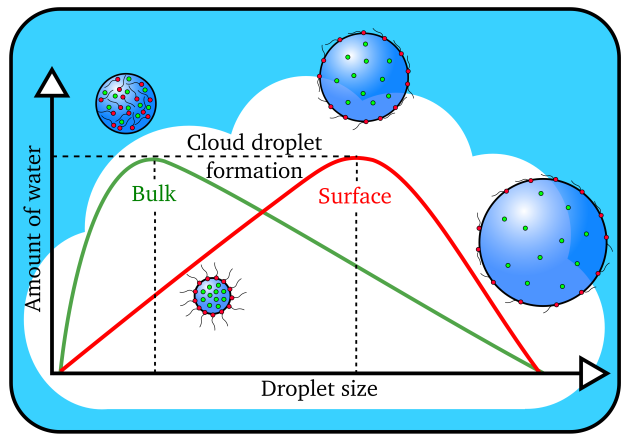
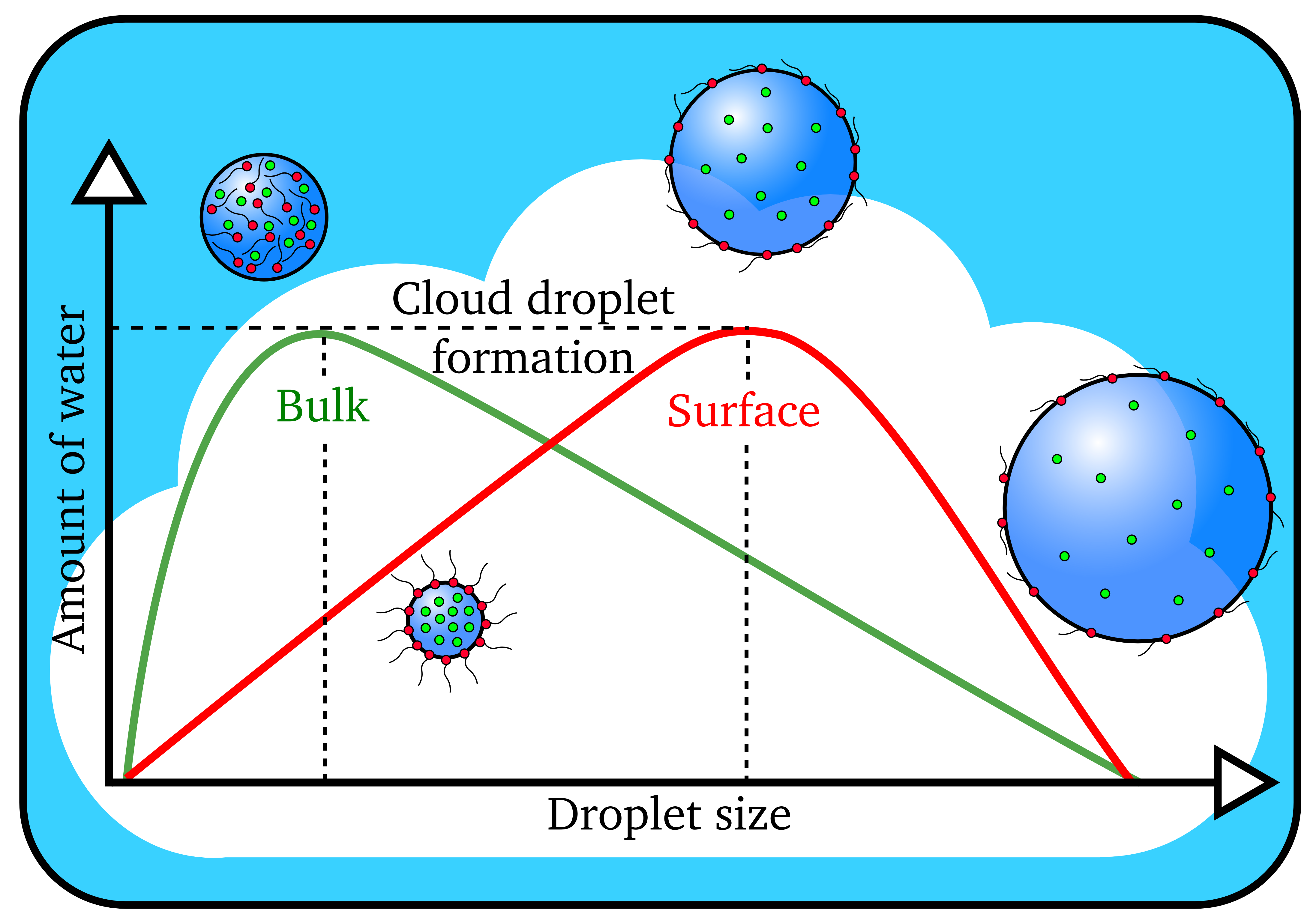
Cloud droplets form when the amount of water vapor reaches a threshold value. Larger cloud droplets form when organic molecules (in red) are present on the surface instead of dissolving in the interior, or bulk, of the droplet. (Image by James Davies, Berkeley Lab)
The scientists determined that organic molecules effectively depressed the surface tension of the water, allowing for more efficient formation of bigger cloud droplets.
“Conventional wisdom says that the water solubility of the aerosol is the key factor in the formation of cloud droplets,” said study senior author Kevin Wilson, the deputy director of science at Berkeley Lab’s Chemical Sciences Division. “The more easily a particle dissolves in water, the easier it is for a cloud droplet to form. What we’re finding is that relying upon solubility alone doesn’t always work. Our study suggests that what the aerosol is doing at the interface with water is what matters in accurately predicting whether it will go on to form cloud droplets.”
The findings, to be published in the March 25 issue of the journal Science, could improve the accuracy of climate change models that predict the potential cooling effect of reflective clouds based upon the particles in the air.
“Accurately describing the connection between the chemistry of aerosol particles and the formation of cloud droplets remains difficult, and it is a key challenge for models to correctly predict climate,” said Wilson.
Wilson worked with study lead author Christopher Ruehl, who did the research while he was a postdoctoral scholar; and co-author James Davies, a current postdoctoral scholar at Berkeley Lab.
The devil’s in the details
The current understanding of how cloud droplets form involves water vapor that encounters cooler air, often at higher altitudes and lower pressure. The vapor then condenses into small droplets of water or ice crystals that comprise clouds.
But the real catalyst in this process is the condensation of water on aerosol particles. These particles, known as cloud condensation nuclei, seed the formation of the cloud droplets. The details surrounding this microphysical process remain unclear, but the belief took hold among many atmospheric scientists and meteorologists that the main factor of significance when cloud droplets formed was the solubility of the aerosol.
These microscopic interactions could have macroscopic effects. The size of the droplets in a cloud affect its brightness. The smaller and more numerous the droplets, the more light gets scattered. Reflecting more light has the effect of cooling Earth’s surface.
Certain inorganic particles, like sea salt, dissolve easily in water, but the atmosphere is typically a complex mixture of organic and inorganic aerosols. Sources of organic aerosols include diesel and gasoline emissions, forests, wildfires and even algal blooms in the ocean.
To account for this mix of particles, the Berkeley Lab researchers conducted experiments using custom-built equipment to model cloud droplet formation. They used dicarboxylic acids, a type of organic compound, and ammonium sulfate, an inorganic salt. They measured the size of the droplets formed when the particles were exposed to water vapor under typical cloud-forming conditions.
“We were finding that the cloud droplets were 50 to 60 percent larger than predicted using standard models that relied upon how easily the particles could dissolve,” said Ruehl, who is now an engineer studying vehicle emissions at the California Air Resources Board. “That’s when we realized something else was going on, so we created a new model.”
By factoring in the effects of surface tension depression, the researchers were able to correctly predict the size of the droplets formed.
“The role of inorganic and organic aerosols in cloud formation has been a highly contentious issue that’s been argued about for many years,” said Wilson. “Based on the paper’s findings, I would say that these surface interactions play a central role in cloud droplet formation, and that they should be considered in climate models.”
Funding for this research came from DOE’s Basic Energy Sciences program.
###
Lawrence Berkeley National Laboratory addresses the world’s most urgent scientific challenges by advancing sustainable energy, protecting human health, creating new materials, and revealing the origin and fate of the universe. Founded in 1931, Berkeley Lab’s scientific expertise has been recognized with 13 Nobel prizes. The University of California manages Berkeley Lab for the U.S. Department of Energy’s Office of Science. For more, visit www.lbl.gov.
DOE’s Office of Science is the single largest supporter of basic research in the physical sciences in the United States, and is working to address some of the most pressing challenges of our time. For more information, please visit science.energy.gov.